Lissette Rosero: 2014

Ecuaciones de rectas y planos.

ECUACIONES DE PLANOS Y RECTAS
Para determinar un plano se necesitan un punto Po(xo,yo,zo) y un vector Ñ(A, B, C) normal al plano. La ecuación del plano viene entonces dada por la relación:
A(x - xo) + B (y - yo) + C (z - zo) = 0 A.x + B.y + C.z + D = 0 (1)
Donde D = -A.x - B.y - C.z
Se pueden considerar varios casos particulares según que uno o dos de los coeficientes de la ecuación (1) sean nulos.
a) Plano paralelo al eje OX. Se tiene A = 0 y la ecuación toma la forma:

b) Plano paralelo al eje OY. Se tiene B = 0 y la ecuación general toma la forma:

c) Plano paralelo al eje OZ. Se tiene C = 0 y la ecuación general toma la forma:

d) Plano que pasa por el origen. Se tiene D = 0 y la ecuación general toma la forma:
A.x + B.y + C.z = 0
e) Plano perpendicular al eje OZ. Se tiene en este caso A = 0, B = 0 y la ecuación general toma la forma:

f) Plano perpendicular al eje OY o, lo que es igual, paralelo al plano XOZ. Se tiene en este caso A = 0, C = 0 y la ecuación general toma la forma:
B.y + D = 0 ; y = Cte
g) Plano perpendicular al eje OX o, lo que es igual, paralelo al plano YOZ. Se tiene en este caso B = 0, C = 0 y la ecuación general toma la forma:
A.x + D = 0 ; x = Cte.
ECUACIÓN VECTORIAL
Ésta expresa una recta en términos de 2 vectores: el vector posición de un punto cualquiera de la recta (<x,y,z>), y el vector dirección de la recta(<a,b,c>) multiplicado por una constante (en este caso lambda). Este último se obtiene fácilmente, con la diferencia de las coordenadas de dospuntos de la misma.
Por ejemplo, para la recta
y = 3x + 8
si sustituimos los valores de x=0 y x=1, obtenemos los dos puntos (0,8) y(1,11).
Restando las coordenadas correspondientes de x e y, 11–8 = 3, 1–0 = 1. Por lo tanto, el vector dirección de la recta es o <1,3>.
Sabiendo que (0,8) es un punto de la recta, podemos escribir su ecuación vectorial de la siguiente forma:
Generalizado para rectas en 3 dimensiones, la que pasa por los puntos (3,6,1) y (2,5,8), tiene vector dirección <2–3, 5–6, 8–1> = ←1,−1,7>, y por lo tanto, su ecuación vectorial podría ser.
Con λ = 0 tenemos el punto (3,6,1), y con λ = 1 se obtiene el (2,5,8).
ECUACIONES PARAMÉTRICAS
Estas podrían considerarse el desarrollo de la ecuación vectorial, ya que representan las coordenadas de un punto de la recta en términos de unavariable independiente λ o t.
Siguiendo con el ejemplo anterior, si tenemos la ecuación vectorial sus ecuaciones paramétricas son
x = 3 + λ( − 1) = 3 – λ
y = 6 + λ( − 1) = 6 – λ
z = 1 + λ(7) = 1 + 7λ
Sustituyendo los mismos valores de lambda que en la ecuación anterior, podemos llegar a los puntos correspondientes.
ECUACIÓN CONTINUA
A estas se llega despejando la variable independiente (λ o t) en las ecuaciones paramétricas, e igualando todas las ecuaciones resultantes. La forma general de la ecuación continua es:
(x-x0)/a=(y-y0)/b
Por lo tanto
Cuando una de las variables no está en términos de la variable independiente (es constante), no se deja en la triple igualación, sino que se coloca aparte, después de un “punto y coma”
Esto significa que en las ecuaciones paramétricas, la variable lambda o tno aparecía en la ecuación de la variable que queda aparte, y por lo tanto, que el vector dirección tiene un componente cero en esa posición.
Para esa última recta, las ecuaciones paramétricas serían
x = 5λ – 4
y = 15λ + 7
z = 5
Y la ecuación vectorial: xxx
ECUACIONES DE RECTA
Recordemos que la derivada representa el valor de la recta tangente, el cual posee una dimensión y contienen varios puntos hasta el infinito. Cuando trabajamos en 3D(3 dimensiones) las ecuaciones de recta son las siguientes:

Nos queda una igualdad de vectores (ternas), y sabemos que para quesean iguales cada componente debe de ser igual, por lo tanto al igualar los componentes nos quedan las ecuaciones paramétricas de la recta en 3 dimensiones.

Despejando t de las ecuaciones Paramétricas, podemos igualar todas las ecuaciones resultantes obteniendo así las Ecuaciones Simétricas.

Coordenadas Cilíndricas

En el sistemas de coordenadas cilíndricas un punto P del espacio tridimensional está representado por la terna ordenada (r,θ,z), donde r y el θ son las coordenadas polares de la proyección de P en el plano xy y z es la distancia dirigida del plano xy a P.

Ecuaciones para transformar de Cilíndricas a Rectangulares

$x(r,\theta,z)=r\cos \left ( \theta \right )$
$y(r,\theta,z)=r\sin \left ( \theta \right )$
$z(r,\theta,z)=z$

Las coordenadas cilíndricas son útiles en problemas que tienen simetría alrededor de un eje, en ese caso se selecciona el eje z de manera que coincida con el eje de simetría

Ecuaciones para transformar de Rectangulares a Cilíndricas

$\theta\left ( x,y,z \right )=\tan^{-1}\left ( \frac{y}{x} \right )$
$r\left ( \ x,y,z \right )= \sqrt{x^{2}+y^{2}}$
$z(x,y,z)=z$

Ecuaciones para transformar de Cilíndricas a Esféricas

$\rho=\sqrt{r^{2}+z^{2}}$
$\theta = \theta$
$\phi =\tan^{-1}\left ( \frac{r}{z}\right )$

El sistema de coordenadas esféricas es especialmente útil en problemas donde hay simetría alrededor de un punto, y el origen se pone en ese punto.

Ejemplo # 1

Convertir el Punto $(3,-3,-7)$ a coordenadas cilíndricas.

Encontramos $r$

$r=\sqrt{3^{2}+(-3)^{2}}\rightarrow \sqrt{18} \rightarrow 3\sqrt{2}$
$\therefore r=3\sqrt{2}$

Ahora encontramos $\theta$

$\theta=\tan^{-1}\left ( \frac{-3}{3} \right )$
$\theta=\tan^{-1}(-1)$ el cuadrante donde $y$ es negativo (-3) y $x$ es positivo (3) es el IV cuadrante.
$\therefore \theta=\tan^{-1}(-1)=-\frac{\pi}{4}$

Ahora encontramos $z$ :
$z = z\;\; z = -7$

Entonces, el punto en coordenadas cilíndricas es: $(3\sqrt{2},-\frac{\pi}{4},-7)$

Ejemplo # 2

Convertir el punto $\left (2,\frac{2\pi}{3},1 \right )$ en coordenadas cilíndricas a coordenadas rectangulares.

Encontremos $x$

$x=2\cos\left(\frac{2\pi}{3}\right)=2\left(-\frac{1}{2}\right)=-1$

Ahora encontremos $y$

$y=2\sin\left( \frac{2\pi}{3}\right)=2\left(\frac{\sqrt{3}}{2}\right)=\sqrt{3}$

Ahora encontremos $z$

$z = z; z = 1$

Entonces, el punto en coordenadas rectangulares es: $(-1,\sqrt{3},1)$

Ejemplo # 3

Escribir la ecuación $z=x^2+y^2$ en coordenadas cilíndricas.

Sabemos que $r^2=x^2+y^2$ entonces sustituimos en la ecuación, obteniendo:

$z=r^2$ y ésta ecuación ya está expresada completamente en coordenadas cilíndricas, pues solo depende de $z,r,$ y $\theta$

Coordenas Esféricas

Las coordenadas esféricas (ρ, θ, φ) de un punto P en el espacio, donde ρ =│OP│ es la distancia del origen a P, θ es el mismo ángulo que en las coordenadas cilíndricas, y φ es el ángulo entre el semieje positivo z y el segmento de recta OP. Note que

                             P≥ 0     0≤φ≤ π

El sistema de coordenadas esféricas es especialmente útil en problemas donde hay simetría alrededor de un punto, y el origen se pone en ese punto.

Dado un vector $r$ del espacio tridimensional y tres planos que se cortan en el punto origen de $r$ , se definen las coordenadas esféricas como los tres números que se obtienen desde las proyecciones ortogonales del vector sobre las tres aristas de intersección de los planos perpendiculares, por las relaciones siguientes:

$x(\rho ,\theta ,\phi)=\rho\cos(\theta)\sin(\phi)$
$y(\rho ,\theta ,\phi)=\rho\sin(\theta)\sin(\phi)$
$z(\rho ,\theta ,\phi)=\rho\cos(\phi)$

Sistema de Coordenadas Esfericas

Es el sistema de coordenadas esféricas un punto p del espacio que viene representado por un trío ordenado $(\rho,\theta,\phi)$ , donde:
1.- $\rho$ es la distancia de P al origen, $\rho><0$ .
2.- $\theta$ es el mismo Angulo utilizado en coordenadas cilíndricas para $r>0$ .
3.- $\phi$ es el Angulo entre el semieje $z$ positivo y el segmento recto $(0,P)$ , $0<\phi>\pi$ .
Nótese que las coordenadas primeras y terceras son siempre no negativas.

Coordenadas Esféricas

Ecuaciones para transformar de Esféricas a Rectangulares

$x(\rho ,\theta ,\phi)=\rho\cos(\theta)\sin(\phi)$
$y(\rho ,\theta ,\phi)=\rho\sin(\theta)\sin(\phi)$
$z(\rho ,\theta ,\phi)=\rho\cos(\phi)$

Ecuaciones para transformar de Rectangulares a Esféricas

$\rho(x,y,z)=\sqrt{x^{2}+y^{2}+z^{2}}$
$\phi(x,y,z)=\tan^{-1}\left ( \frac{\sqrt{x^{2}+y^{2}}} {z} \right )$
$\theta(x,y,z)=\tan^{-1} \left ( \frac{y}{x}\right )$

Ecuaciones para transformar de Esféricas a Cilíndricas

$r=\rho \sin \phi$
$\theta = \theta$
$z=\rho \cos \phi$

Ejemplo # 4

Convertir el punto $\left(2,\frac{\pi}{4},\frac{\pi}{3}\right)$ a coordenadas rectangulares.

$x=2\sin\left(\frac{\pi}{3}\right)\cos\left(\frac{\pi}{4}\right) =2\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{\sqrt{2}}\right)=\sqrt{\frac{3}{2}}$

$y=2\sin\left(\frac{\pi}{3}\right)\sin\left(\frac{\pi}{4}\right) =2\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{\sqrt{2}}\right)=\sqrt{\frac{3}{2}}$

$z=2\cos\left(\frac{\pi}{3}\right)=2\left(\frac{1}{2}\right)=1$

$\therefore$ El punto en coordenadas rectangulares es: $\left(\sqrt{\frac{3}{2}},\sqrt{\frac{3}{2}},1 \right )$ .

Ejemplo # 5

Convertir la ecuación rectangular a coordenadas cilíndricas.

$x^2+y^2+z^2=16$

$r^2=x^2+y^2$

$z=z$

$r^2+z^2=16$

Ejemplo # 6

Convertir la ecuación rectangular a coordenadas esféricas.

$x^2+y^2+z^2=16$

$\rho=\sqrt{x^{2}+y^{2}+z^{2}}$

$\rho^2=16$

Ejemplo # 7

Describa la superficie cuya ecuación en coordenadas cilíndricas es z=r. Solución La ecuación dice que el valor z, o altura, de cada punto sobre la superficie es igual que r, la distancia del punto al eje z. Como θ no aparece, puede variar. Por lo tanto, cualquier trazo horizontal en el plano z+ k (K>)) es un circulo de radio k. estas trazas sugieren que la superficie es un cono. Esta predicción puede confirmarse si se convierte la ecuación en coordenadas rectangulares. De la primera ecuación tenemos
$\ z^2=r^2= x^2+y^2$

Límites y continuidad

Sean

\mathbf{a} \in \mathbb{R}^n

\mathbf{b} \in \mathbb{R}^m.

Escribimos:

\lim_{\mathbf{x} \to \mathbf{a}}\mathbf{f}\big (\mathbf{x}\big )=\mathbf{b}

o bien,

\mathbf{f}(\mathbf{x}) \rightarrow \mathbf{b}

cuando

\mathbf{x} \rightarrow \mathbf{a}

para expresar lo siguiente:

\lim_{\big \|\mathbf{x-a}\big \| \to 0}\big \|\mathbf{f}\big (\mathbf{x}\big ) - \mathbf{b}\big \| = 0

donde

\big \|\mathbf{x}\big \|

es la norma euclídea de

\mathbf{x}

. Expresándolo en función de las componentes de

\mathbf{x} = \big (x_1,\ldots,x_n\big ), \mathbf{a} = \big (a_1,\ldots,a_n\big ),

\lim_{\big (x_1,\ldots,x_n\big ) \to \big (a_1,\ldots,a_n\big )}\mathbf{f}\big (x_1,\ldots,x_n\big ) = \mathbf{b}

o, de forma equivalente,

\lim_{\mathbf{x} \to \mathbf{a}}\mathbf{f}\big (\mathbf{x}\big ) = \mathbf{b}

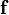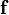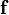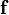Decimos que una función $\mathbf{f}$ es continua en $\mathbf{a} \Leftrightarrow \lim_{\mathbf{x}\to \mathbf{a}}\mathbf{f}\big (\mathbf{x}\big ) = \mathbf{f}\big (\mathbf{a}\big )$

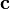$\lim_{\mathbf{x} \to \mathbf{a}}\mathbf{f}\big (\mathbf{x}\big ) = \mathbf{b}, \lim_{\mathbf{x}\to\mathbf{a}}\mathbf{g}\big (\mathbf{x}\big ) = \mathbf{c} \Rightarrow$

a) $\lim_{\mathbf{x} \to \mathbf{a}}\big [\mathbf{f} + \mathbf{g}\big ]\big (\mathbf{x}\big ) = \mathbf{b} + \mathbf{c}$
b) $\lim_{\mathbf{x} \to \mathbf{a}}\lambda\mathbf{f}\big (\mathbf{x}\big ) = \lambda\mathbf{b} \quad\forall\lambda \in \mathbb{R}$
c) $\lim_{\mathbf{x} \to \mathbf{a}}\big (\mathbf{f}\cdot\mathbf{g}\big )\big (\mathbf{x}\big ) = \mathbf{b}\cdot\mathbf{c}$
(producto escalar de $\mathbf{b}$ con $\mathbf{c}$ ).
d) $\lim_{\mathbf{x} \to \mathbf{a}}\Big \|\mathbf{f}\big (\mathbf{x}\big )\Big \|=\big \|\mathbf{b}\big \|$

Demostración

Sean $\mathbf{f}$ y $\mathbf{g}$ dos funciones tales que la función compuesta $\mathbf{f}\circ\mathbf{g}$ está definida en $\mathbf{a}$ , siendo

$\big (\mathbf{f}\circ\mathbf{g}\big )\big (\mathbf{x}\big ) = \mathbf{f}\Big [\mathbf{g}\big (\mathbf{x}\big )\Big ]$
$\mathbf{g}$ es continua en $\mathbf{a}$ y $\mathbf{f}$ es continua en $\mathbf{g}\big (\mathbf{a}\big ) \Rightarrow \big (\mathbf{f}\circ\mathbf{g}\big )$ es continua en $\mathbf{a}$ .

Lissette Rosero

Archivo del Blog

lunes, 14 de julio de 2014

INTRODUCCION

domingo, 13 de julio de 2014

PRIMERA SEMANA